Cyklus úvah o teoretických základech
cyklistiky
1. PÁTRÁNÍ PO PRAVDĚ O PRŮMĚRNÉ
RYCHLOSTI
(óda
na seriál Časovek do kopce)
Nejdřív se zamyslete, kým vlastně jste!
Pohodáři, které nikdy
nezajímá, jak dojedete? Šílenci, jejichž průměrná rychlost je nad počitatelnými
limitami? Matematici, pro které nejsou žádná teoretická zákoutí překvapením?
Exoti, nehodící se mezi nás obyčejné smrtelníky? Pak se nezdržujte a opusťte tuto stránku.
Vás ostatní zvu do světa
teoretických základů cyklistiky, který můžete opustit kdykoli jakmile zjistíte,
že jste intelektuálně dále, než autor tohoto pojednání.
Také se Vám při monotónní jízdě a častém sledování computeru
zdá, že by průměrná rychlost měla být vyšší? Mě se to stává dost pravidelně.
Jen na krátký úsek jsem donucen zpomalit a průměrná rychlost klesá jako divá,
naproti tomu stejný úsek vysokou rychlostí zvedne průměr jen o málo.
Jaké jsou důvody tak podlého chování průměrné rychlosti?
Sama za nic nemůže, je totiž závislá na čase.
Vezměme si tedy modelový příklad. Pro zjednodušení průjezd
trasou vedoucí nejdříve 10 km do kopce a následně stejných 10 km z kopce –
pohlédněte na graf 1:

Graf 1 – Profil modelové trasy
Do kopce pojedu stálou rychlostí pouze 10 km/hod a
z kopce pak 40 km/hod.
Při prostém vynesení jízdních rychlostí
v závislosti na vzdálenosti do grafu bychom očekávali průměrnou rychlost
logicky v půli mezi 10 a 40 km/hod, tedy 25 km/hod (nediskutujme o
rychlosti - někdo do kopce zpomalí na 40 km/hod, já zpomalím na 10 km/hod) -
pohlédněte na graf 2:
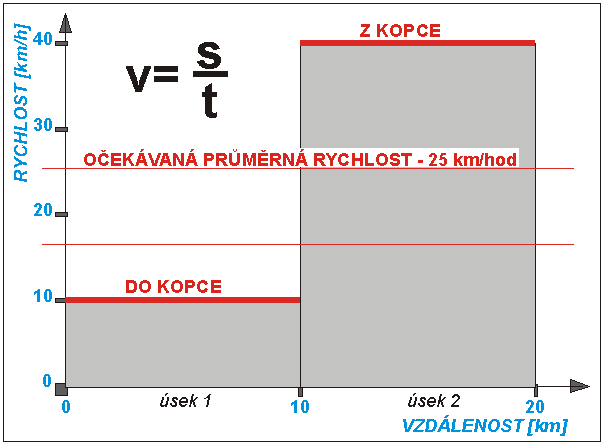
Graf 2 – Rychlostní poměry
na trase
Průměrná rychlost však dle základního vzorce v=s/t závisí
na vzdálenosti a čase (zapomeňme, že v reálném případe jsou to navíc
derivace):
v=s/t => s=v*t
Průměrnou rychlost je tedy nutno zjišťovat v grafu 3:
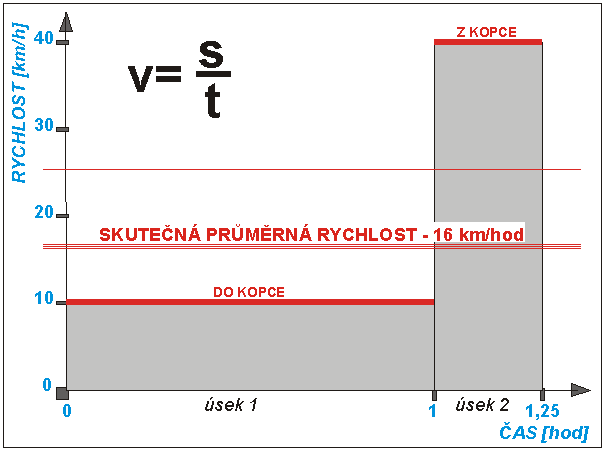
Graf 3 – Rychlostní poměry v závislosti na čase
Z tohoto grafu bohužel vyplývá, že úseky projeté vyšší
rychlostí trvají kratší dobu, což je logické a o to méně ovlivňuje průměrnou
rychlost, což je nepříjemné. Vypadá to skoro tak, že není důvod jezdit rychle,
protože čím vyšší rychlost, tím kratší čas trvá projetí úseku a tím omezeněji
se tento úsek podílí na zvýšení průměrné rychlosti. Samozřejmě, čím vyšší
rychlost v rychlém úseku (úsek 2), tím vyšší průměrná rychlost. Ovšem
nárůst rychlosti při velmi vysoké rychlosti v rychlém úseku 2 oproti
pomalému úseku (úsek 1) se již k vašemu zklamní na změně průměrné
rychlosti téměř neprojeví.
Kde je tedy hranice rentability rychlé jízdy? Jak je to
s matematickou teorií?
Už bylo uvedeno, že základním vztahem je v = s / t
a pro průměrnou rychlost platí vf = (s1
+ s2) / (t1 + t2).
Předpokládejme nyní pro jednoduchost dva stejné úseky s1=s2
a pro poměr rychlostí v úseku 1 a 2 mějme koeficient k: v2 = k . v1 =>
t2 = t1 / k
Pak můžeme vztah vf = (s1
+ s2) / (t1 + t2) napsat jako vf = 2s1
/ (t1 + t1/k) a tento
dále upravit na vf = 2k / (k
+ 1) * s1 / t1
=> vf = 2k / (k
+ 1) * v1 .
Zde výraz 2k /
(k + 1) určuje, jak
závisí vf na poměru
rychlostí v jednotlivých úsecích v1 a v2. Tuto závislost vyneseme
do tabulky 1 a grafu 4:
|
Rychlost
v1 |
Rychlost
v2 |
Průměrná
rychlost vf |
|
10 |
10 |
10,0 |
|
10 |
20 |
13,3 |
|
10 |
30 |
15,0 |
|
10 |
40 |
16,0 |
|
10 |
50 |
16,7 |
|
10 |
60 |
17,1 |
|
10 |
70 |
17,5 |
|
10 |
80 |
17,8 |
|
10 |
90 |
18,0 |
|
10 |
100 |
18,2 |
Tabulka 1 – Vliv
rychlosti v2 v úseku s2 na velikost průměrné
rychlosti vf
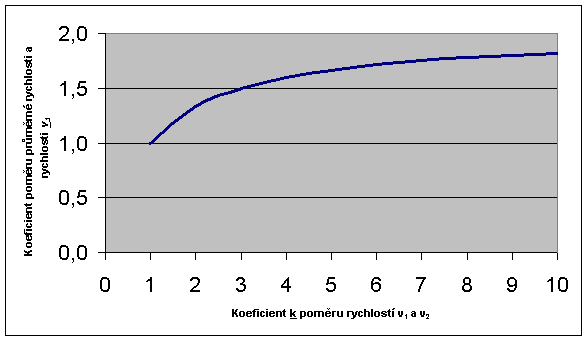
Graf 4 – Závislost
velikosti průměrné rychlosti
na poměru rychlostí
v úsecích s1 a s2.
Z grafu 4 vyplývá, že koeficient zvýšení průměrné
rychlosti nepřekročí nikdy poměr 2 (blíží se limitně k hodnotě 2 pro velmi
veliké hodnoty poměru k jednotlivých rychlostí v1
a v2) a že toto zvyšování se pro poměr k > 3 už
přestává vyplácet (mnohem více se nadřete a průměrná rychlost se moc nepohne).
Z tabulky pak můžeme
pro náš modelový případ odečíst následující údaje: zvýšíme-li rychlost
v úseku 2 vždy o 10 km/hod, pak při zvýšení z 20 na 30 km/hod dojde
ke zvýšení průměrné rychlosti ještě o 1,7 km/hod, při zvýšení z 30 na 40
km/hod se průměrná rychlost zvýší již jen o 1,0 km/hod a při zvýšení z 90
na 100 km/hod již jen o 0,2 km/hod.
Jak již bylo uvedeno, při rychlosti v úseku 1 - 10 km/hod
a v úseku 2 – 40 km/hod je průměrná rychlost 16,0 km/hod. Pokud by
se nám podařilo zvýšit rychlost v úseku 2 4x na šílených 80 km/hod, stoupne průměrná
rychlost pouze na 17,8 km/hod, tedy o 1,8 km/hod. Podaří-li se nám však
úsek 2 protáhnout z 10 km na 40 km, tedy také 4x, vzroste průměrná
rychlost již na 25 km/hod, tedy o 9 km/hod a to už je zajímavější.
Docházíme tedy
k závěru, že je výhodnější snažit se o stálou vyšší okamžitou rychlost,
než v náročných úsecích výrazně zpomalit a pak dohánět průměr ďábelsky
rychlou jízdou z kopce.
A také se dostáváme k tomu, co bylo naznačeno již na
počátku. Účastněte se pravidelně Časovek do kopce
- pomáhají vám natrénovat vyšší rychlosti v náročných úsecích a dosáhnout
tak vyšších průměrných rychlostí. Nebezpečně šílenou jízdou z kopce
získáte méně, než očekáváte.
Nakonec se vám, kteří jste
dočetli až sem, omlouvám za snůšku suché teorie a radím – vypněte počítač,
namažte kolo shora dolů a hurá na trénink do kopců (o vlivu mazání snad někdy
příště).
Cyklisticko-matematickou logiku pro vás uchopil a sepsal
Dušan PŘÍBRSKÝ,
Logistik KPO
pod laskavým patronátem a pobídkami
Jirky SLADKÉHO,
Prezidenta KPO