Užitečný malý hmyz
V běžném životě vyjadřujeme hmotnost v kilogramech a gramech, koncentraci roztoku potom v procentech, ve výjimečném případě v gramech na litr. Tomu všichni rozumíme a máme o tom jakous takous představu. V biochemii a medicíně se ale u koncentrací používá jednotka milimol na litr – mmol/l.
Jak si jí můžete představit a kde hledat její přínos? Jak všichni víte už od mateřské školy, kilo železa váží ale úplně na chlup stejně jako kilo peří – to znamená, že obsahuje stejné množství hmoty. V biochemii nás někdy nezajímá celkové množství hmoty, ale kolik to množství představuje základních jednotek – molekul. Když to trochu zjednoduším: jeden gram látky s molekulou velikosti 10 obsahuje desetkrát méně molekul než gram látky s molekulou velikosti 1. Otočeno naruby – jeden gram látky velikosti molekuly 1 obsahuje 10 mmol, jeden gram látky o velikosti molekuly 10 pak obsahuje 1 mmol.
Proč taková komplikace? Představte si reakci, ve které sloučením látky A a B vzniká látka C: A + B -> C. V gramech při vám jistě známém zákoně zachování hmoty platí 1g A + 1g B= 2g C. Kdo si ovšem myslí, že 1 mmol A + 1 mmol B -> 2 mmol C, myslí si špatně. Z jedné molekuly A a jedné molekuly B vznikne jedna velká molekula C! Naopak, pokud známe reakci a zajímáme se jen o jeden konkrétní produkt, můžeme říci že v reakci C -> A + B vznikne z jednoho mmol C jeden mmol A, aniž bychom se starali o jejich faktické hmotnosti. Jednu takovou reakci jsme už potkali – z jednoho mmol glukózy vznikne bez přístupu kyslíku jeden mmol laktátu, i když se z glukózy něco odtrhne a spálí na energii. Díky jednotce mmol tak dokážeme vyčíslit daleko lépe energetické zisky či nároky reakcí.
Stejně tak můžeme díky jednotce mmol/l usuzovat na chování roztoků. Naše tělo je totiž v jednom ze zjednodušujících pohledů velký vak, rozdělený na spoustu malých a ještě menších vaků, naplněných různými roztoky. Chování roztoků a přesuny mezi jednotlivými pytlíky závisí na rozpuštěném počtu molekul daleko více než na hmotnosti rozpuštěných látek.
Určitě jste už, alespoň v souvislosti s iontovými nápoji, slyšeli pojem “izotonický roztok”. To je takový roztok, který v jednom litru obsahuje stejně molekul jako tekutá složka krve – plazma (přesně řečeno sérum, ale to by bylo na dlouhé povídání). Pokud budeme takový roztok vyrábět z glukózy, musíme připravit 5% roztok, tedy rozpustit 5 g glukózy v 95 ml vody. Pokud budeme ale vyrábět takzvaný fyziologický roztok, stačí nám rozpustit pouhých 0,9 g kuchyňské soli (NaCl) v 99,1 ml vody, tedy 0,9% roztok! Výsledná “tonicita” obou roztoků je přitom stejná – 300 mOsmol. Jak je to možné? Pět gramů glukózy je přesně 300 mmol. Devět desetin gramu soli je sice jen 150 mmol, při rozpouštění se ale sodík (Na) a chlor (Cl) od sebe oddělí – disociuje (fuj, to slovo ale vypadá blbě!) na 150 mmol Na+ a 150 mmol Cl- - dohromady opět 300. Ti z vás, kdo si pamatují, že molekula maltodextrinu vznikne spojením pěti molekul glukózy, mají první příklad energetického roztoku. Izotonický roztok maltodextrinu obsahuje 25 g maltodextrinu při “tonicitě” 300 mOsmol, tedy 5x více energie, než izotonický roztok glukózy! Znovu se k míchání iontových a energetických nápojů vrátíme v kapitole o potravinových doplňcích.
Tady měla vsuvka původně končit. Jenže mezitím vyšel nový Peloton (6/02) a v poloreklamním článku ing. Havlíčka se objevily drobné nesrovnalosti. Protože o iontových a energetických článcích budu psát, cítím potřebu alespoň některé pavučiny vysmýčit za čerstva, dokud ještě příliš nelpí.
Zatím se otřu jen o fakta, vztahující se k tabulce číslo 1 - denní spotřebě vody a základních minerálů sodíku a draslíku. Abyste jí nemuseli hledat, doslovně jí přepisuji:
| Voda | 2 – 3 kg (včetně vody v potravinách) |
| Sodné ionty | 100 – 200 mOsmol |
| Draselné ionty | 60 – 80 mOsmol |
| Orientační podíl sodíku a draslíku | 5:2 |
Proti tvrzení o 2 – 3 kg vody v zásadě námitky nemám, i když si myslím, že 1,5 ž 2,5 l vody na den plus 500 g v potravě je pro vytrvalostní aktivity dost málo.
Ovšem udávat potřebu solí v miliosmolech je asi totéž, jako udávat délku schodiště v ceně běhounu, který ho pokrývá. Miliosmoly jsou jednotkou osmotické aktivity, nikoliv osmotického tlaku, jak kolega mylně uvádí. Osmotický tlak se udává jako každý jiný tlak v Pascalech.
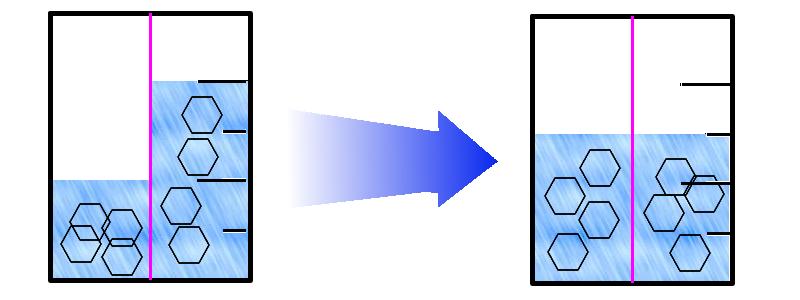
Co znamená osmotická aktivita doopravdy? Podrobný a stravitelnější výklad vás ještě čeká. Zatím jen velmi zkratkovitě. Představte si litrovou nádobu, rozdělenou na dvě stejné nádrže polopropustnou membránou. Polopropustná znamená, že propouští pouze rozpouštědlo, v našem případě vodu, nikoliv už rozpuštěnou látku – v našem příkladu to může být třeba glukóza. Nachystáme si dva roztoky. V prvním rozpustíme čtyři milimoly do jednoho litru, ve druhém čtyři milimoly do půl litru. Máme tedy stejné množství glukózy – po čtyřech milimolech. V milimolech na litr je to ale v prvním 4 mmol/l, ve druhém 8 mmol na litr. V roztoku jedné látky se jeho osmotická aktivita rovná jeho koncentraci v mmol/kg, v případě vody je to prakticky stejné jako mmol/l (tady jsme narazili na další nepravdu v článku – osmotická aktivita se dá většinou vypočítat naprosto přesně součtem molárních koncentrací jednotlivých rozpuštěných látek. Kde to neplatí, si také řekneme za chvíli).
Výsledná osmotická aktivita je u prvního roztoku 4 mOsmol, u druhého 8 mOsmol. Teď každý roztok nalijeme do jedné poloviny naší nádoby. A začnou se dít věci! Příroda nemá ráda nerovnováhu a tak hustší roztok začne přes membránu nasávat vodu, tak dlouho, dokud se molární koncentrace nevyrovnají. Tlak, kterým nasává (technicky zvaný cuc) je právě onen osmotický tlak, udávaný prachsprostě v Pascalech. Na konci našeho pokusu bude v obou polovinách nádoby koncentrace 6 mmol/l, osmotická aktivita 6 mOsmol, hustší roztok získá 1/4 litru vody, zatímco řidší jí 1/4 litru ztratí. Glukóza, jak jsme si už řekli, membránou neproleze, takže v obou polovinách zůstává stále stejné množství glukózy – 4 mmol.
Pro nevěřící Tomáše, různé vrtáky a štouraly podotýkám a upřesňuji: nejde o spojené nádoby! Kdybychom do jedné poloviny nalili půllitr čisté vody a do druhé litr čisté vody, hladiny by se ani nehnuly. Totéž platí v případě, že by byly v obou polovinách stejně husté roztoky glukózy! Pouze rozdílná osmotická aktivita má tu magickou moc protáhnout vodu zdí! Divné, co?
Pro čtenáře s obrazovou představivostí jsem namaloval obrázek:

Co z toho tedy vyplývá? Tvrzení, že denní potřeba sodíku je 100 mOsmol je nesmysl. Kdybychom to chtěli vypít v jedné “decce”, stačilo by nám 10 mmol, v litru už by milimolů muselo být 100 a pokud bychom sůl chtěli jíst po lžičkách, nestačil by nám solný důl. Nerozpuštěná sůl totiž logicky žádné mOsmoly nemá – není roztokem. Totéž v bledě modrém platí i pro další řádek o draslíku. Když přepočítám milimoly na gramy chloridu sodného jako nejobvyklejšího zdroje sodíku, vychází nám jeden milimol jako 0,058 g a 100 mmol tedy 5,8 g soli na den, což opravdu odpovídá.
Jak bych tedy napsal tabulku já?
| Voda | 2 – 3 l (včetně vody v potravinách) |
| Sodné ionty | 100 – 200 mmol (např. ve 3 - 6 g soli) |
| Draselné ionty | 60 – 80 mmol (např. v 4,5 – 6 g KCl) |
| Orientační podíl sodíku a draslíku | 5:2 |
Proč původní tabulka vznikla právě ve své podobě, je otázka. Vím možná o jednom motivu. Oněch 5 g soli, zahrnující celý denní doporučený příjem, je jedna jediná - zdaleka ne vrchovatá - kávová lžička. To ale nepočítáme příjem z běžné, nepřisolované stravy, která nám uhradí leckdy ještě více, než oněch 5 g. Učebnice sportovní medicíny, které jsou - alespoň zatím - nezávislé na výrobcích suplementů a peněz z jejich reklam, udávají, že i při několikahodinových sportovních výkonech jsou ztráty minerálů bohatě nahrazeny běžnou stravou. Další zajímavostí je, že Reg-Ge drink Unisport (v článku naprosto "nenápadně" propagovaný) obsahuje při středním ředění 1:50 (10 ml v 1/2 l nápoje) v jednom půllitrovém bidonu 19,6 mg sodíku, tedy v nejlepším případě 0,84% denních ztrát! Množství, které nás nepochybně zachrání před křečemi a jinými následky pocení! Ovšem pokud se vše zaobalí vědou a nesrozumitelnými jednotkami, vypadá to hned jinak. Pořád tedy platí heslo cyklistických profesionálů “Vodou k vítězství”.
Abych nebyl nařčen z předpojatosti – Reg-Ge drink vozím také. Většina příchutí mi docela chutná a nepálí po něm žáha. Víc od něj nechci a nečekám.
A ještě jsem slíbil vyvrácení nevypočitatelnosti osmolality roztoku. To platí jen v případě takzvaných elektrolytů – roztoků solí, které disociují – ve vodě se rozkládají na kladně a záporně nabitou část (iont). Příkladem je kuchyňská sůl (viz výše). Teoretická osmolalita roztoku 150 mmol NaCl je 300 mOsmol – 150 Na+ a 150 Cl-. Fakticky ale nedisociují všechny molekuly. Při této koncentraci a teplotě 37 stupňů je reálná osmolalita okolo 280 mOsmol – 10 mmol nedisociuje. Představte si to tak, že sůl se snaží zabírat v roztoku méně místa a vytvářet tak de facto méně nasycený roztok. Přidáte-li do roztoku cokoliv dalšího, další molekuly NaCl zruší disociaci a podíl NaCl na celkové osmolalitě klesne více, než by odpovídalo matematickému poměru. Osmolalita roztoku také klesne v případě, že roztok ochladíte a naopak vzroste při zahřátí.
O roztocích neelektrolytů (to jsou třeba všechny roztoky cukrů) to ale neplatí. Tam odpovídá osmolalita přesně součtu molárních koncentrací všech rozpuštěných složek. U iontově-energetických nápojů, kde většinu osmotické aktivity netvoří soli, ale různé cukry a podobné nedisociující látky, je podle mého názoru vliv disociace zanedbatelný.
A nakonec si neodpustím malou škodolibost. V tomtéž článku v Pelotonu se vyskytuje jedna velmi častá chyba českých učebnic a moje "spisovatelská" noční můra – důkaz v kruhu. Tentokrát nebudu citovat. Za domácí úkol z pilnosti hledejte a najděte. Mým zbožným přáním je, abych se tohoto prohřešku ve svých článcích nedopouštěl.
Váš
Ondra Vojtěchovský
vojtechovsky@kpo.cz